Prayer Times Calculation
From Pray Times
m (→Definitions) |
m (→Definitions) |
||
| Line 34: | Line 34: | ||
|- | |- | ||
! Midnight | ! Midnight | ||
| - | | The mean time from sunset to sunrise (or from | + | | The mean time from sunset to sunrise (or from Sunset to Fajr, in some schools of thought). |
|} | |} | ||
Revision as of 12:59, 29 March 2018
Muslims perform five prayers a day. Each prayer is given a certain prescribed time during which it must be performed. This document briefly describes these times, and explains how they can be calculated mathematically.
Contents |
Definitions
To determine the exact time period for each prayer (and also for fasting), we need to determine nine points of time per a day. These times are defined in the following table:
| Time | Definition |
|---|---|
| Fajr | When the sky begins to lighten (dawn). |
| Sunrise | The time at which the first part of the Sun appears above the horizon. |
| Dhuhr | When the Sun begins to decline after reaching its highest point in the sky. |
| Asr | The time when the length of any object's shadow reaches a factor (usually 1 or 2) of the length of the object itself plus the length of that object's shadow at noon. |
| Sunset | The time at which the Sun disappears below the horizon. |
| Maghrib | Soon after sunset. |
| Isha | The time at which darkness falls and there is no scattered light in the sky. |
| Midnight | The mean time from sunset to sunrise (or from Sunset to Fajr, in some schools of thought). |
The next section provides information on how to calculate the above times mathematically for any location if the coordinates of the location are known.
Astronomical Measures
There are two astronomical measures that are essential for computing prayer times. These two measures are the equation of time and the declination of the Sun.
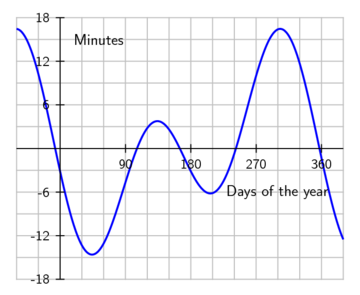
The equation of time is the difference between time as read from a sundial and a clock. It results from an apparent irregular movement of the Sun caused by a combination of the obliquity of the Earth's rotation axis and the eccentricity of its orbit. The sundial can be ahead (fast) by as much as 16 min 33 s (around November 3) or fall behind by as much as 14 min 6 s (around February 12), as shown in the following graph:
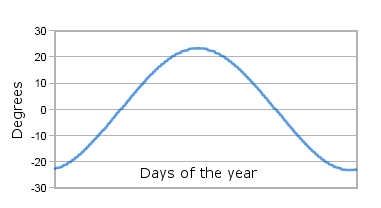
The declination of the Sun is the angle between the rays of the sun and the plane of the earth equator. The declination of the Sun changes continuously throughout the year. This is a consequence of the Earth's tilt, i.e. the difference in its rotational and revolutionary axes.
The above two astronomical measures can be obtained accurately from The Star Almanac, or can be calculated approximately. The following algorithm from U.S. Naval Observatory computes the Sun's angular coordinates to an accuracy of about 1 arcminute within two centuries of 2000.
d = jd - 2451545.0; // jd is the given Julian date g = 357.529 + 0.98560028* d; q = 280.459 + 0.98564736* d; L = q + 1.915* sin(g) + 0.020* sin(2*g); R = 1.00014 - 0.01671* cos(g) - 0.00014* cos(2*g); e = 23.439 - 0.00000036* d; RA = arctan2(cos(e)* sin(L), cos(L))/ 15; D = arcsin(sin(e)* sin(L)); // declination of the Sun EqT = q/15 - RA; // equation of time
Calculating Prayer Times
To calculate the prayer times for a given location, we need to know the latitude (L) and the longitude (Lng) of the location, along with the local Time Zone for that location. We also obtain the equation of time (EqT) and the declination of the Sun (D) for a given date using the algorithm mentioned in the previous section.
Dhuhr
Dhuhr can be calculated easily using the following formula:
Dhuhr = 12 + TimeZone - Lng/15 - EqT.
The above formula indeed calculates the midday time, when the Sun reaches its highest point in the sky. A slight margin is usually considered for Dhuhr as explained in this note.
Sunrise/Sunset
The time difference between the mid-day and the time at which sun reaches an angle α below the horizon can be computed using the following formula:
Astronomical sunrise and sunset occur at α=0. However, due to the refraction of light by terrestrial atmosphere, actual sunrise appears slightly before astronomical sunrise and actual sunset occurs after astronomical sunset. Actual sunrise and sunset can be computed using the following formulas:
Sunrise = Dhuhr - T(0.833),
Sunset = Dhuhr + T(0.833).
If the observer's location is higher than the surrounding terrain, we can consider this elevation into consideration by increasing the above constant 0.833 by 0.0347 × sqrt(h), where h is the observer's height in meters.
Fajr and Isha
There are differing opinions on what angle to be used for calculating Fajr and Isha. The following table shows several conventions currently in use in various countries (more information is available at this page).
| Convention | Fajr Angle | Isha Angle |
|---|---|---|
| Muslim World League | 18 | 17 |
| Islamic Society of North America (ISNA) | 15 | 15 |
| Egyptian General Authority of Survey | 19.5 | 17.5 |
| Umm al-Qura University, Makkah | 18.5 | 90 min after Maghrib 120 min during Ramadan |
| University of Islamic Sciences, Karachi | 18 | 18 |
| Institute of Geophysics, University of Tehran | 17.7 | 14* |
| Shia Ithna Ashari, Leva Research Institute, Qum | 16 | 14 |
* Isha angle is not explicitly defined in Tehran method.
For example, according to Muslim World League convention, Fajr = Dhuhr - T(18) and Isha = Dhuhr + T(17).
Asr
There are two main opinions on how to calculate Asr time. The majority of schools (including Shafi'i, Maliki, Ja'fari, and Hanbali) say it is at the time when the length of any object's shadow equals the length of the object itself plus the length of that object's shadow at noon. The dominant opinion in the Hanafi school says that Asr begins when the length of any object's shadow is twice the length of the object plus the length of that object's shadow at noon.
The following formula computes the time difference between the mid-day and the time at which the object's shadow equals t times the length of the object itself plus the length of that object's shadow at noon:
Thus, in the first four schools of thought, Asr = Dhuhr + A(1), and in Hanafi school, Asr = Dhuhr + A(2).
Maghrib
In the Sunni's point of view, the time for Maghrib prayer begins once the Sun has completely set beneath the horizon, that is, Maghrib = Sunset (some calculators suggest 1 to 3 minutes after Sunset for precaution). In the Shia's view, however, the dominant opinion is that as long as the redness in the eastern sky appearing after sunset has not passed overhead, Maghrib prayer should not be performed. It is usually taken into consideration by assuming a twilight angle like Maghrib = Dhuhr + T(4).
Midnight
Midnight is generally calculated as the mean time from Sunset to Sunrise, i.e., Midnight = 1/2(Sunrise - Sunset). In Shia point of view, the juridical midnight (the ending time for performing Isha prayer) is the mean time from Sunset to Fajr, i.e., Midnight = 1/2(Fajr - Sunset).
Higher Latitudes
In locations at higher latitude, twilight may persist throughout the night during some months of the year. In these abnormal periods, the determination of Fajr and Isha is not possible using the usual formulas mentioned in the previous section. To overcome this problem, several solutions have been proposed, three of which are described below.
- Middle of the Night
- In this method, the period from sunset to sunrise is divided into two halves. The first half is considered to be the "night" and the other half as "day break". Fajr and Isha in this method are assumed to be at mid-night during the abnormal periods.
- One-Seventh of the Night
- In this method, the period between sunset and sunrise is divided into seven parts. Isha begins after the first one-seventh part, and Fajr is at the beginning of the seventh part.
- Angle-Based Method
- This is an intermediate solution, used by some recent prayer time calculators. Let α be the twilight angle for Isha, and let t = α/60. The period between sunset and sunrise is divided into t parts. Isha begins after the first part. For example, if the twilight angle for Isha is 15, then Isha begins at the end of the first quarter (15/60) of the night. Time for Fajr is calculated similarly.
In case Maghrib is not equal to Sunset, we can apply the above rules to Maghrib as well to make sure that Maghrib always falls between Sunset and Isha during the abnormal periods.
Implementation
The formulas described above are implemented completely and can be obtained in various programming languages from this page.
References
- The Determination of Salat Times, by Dr. Monzur Ahmed.
- Approximate Solar Coordinates, by U.S. Naval Observatory.
- The Islamic Prayer Times, by Professor Tariq Muneer.
- Wikipedia, the free encyclopedia.